목차
- Causal Impact란?
- Bayesian structural time series (BSTS)
1. Causal Impact란?
직역하면 인과 영향이라는 뜻이다. 처음에는 Causal Inference (인과 추론)과 개념이 혼동되어서 햇깔리는 부분이 있었다. Inference와 Impact가 어떤 차이가 있는지 짚고 넘어가도록 하겠다.
- Causal Inference
- 정의: 원인과 결과 간의 인과 관계를 추론하려는 통계적 기법과 방법론
- 목적: 특정 처리 변수 또는 이벤트가 다른 변수에 미치는 인과적 영향을 추정
- 사용되는 방법: 다양한 통계적 모델링 기법이 사용되며, 실험적인 설계 (Randomized Controlled Trials, RCTs) 또는 관측적인 데이터에서의 처리 효과를 추론하는 방법이 포함됨
- Causal Impact
- 정의: 특정 이벤트 또는 처리 변수의 발생이 시계열 데이터에 미치는 영향을 분석하기 위한 모델링 기법
- 목적: 특정 이벤트가 발생한 후의 시계열 데이터와 발생하기 전의 데이터를 비교, 이벤트 영향 정량화
- 사용되는 방법: BSTS 모델 기반, 사전/사후 비교를 통해 특정 이벤트의 영향 추정
Causal Inference는 원인과 결과 간의 일반적인 인과적 원리를 다루는 통계적 추론의 영역이며, Causal Impact는 특정 이벤트의 발생이 시계열 데이터에 미치는 영향을 분석하는 구체적인 모델링 기법이다. 본 포스트에서는 Causal Impact에 대해서 더 자세히 다뤄 볼 예정이다.
2. Bayesian structural time series (BSTS)
구조적 베이지안 시계열 방법으로 직역할 수 있다. 시계열 데이터를 '구조적 베이지안' 이라는 방법으로 분석한다고 해석할 수도 있다. 그렇다면 구조적 베이지안 방법이라는 것은 어떤 것일까?
시계열 분석에서 사용되는 통계적 접근 방식에는 크게 두 가지 방법이 존재한다.
- 빈도주의
- 얼마나 자주 특정 사건이 반복되어 발생하는지에 집중
- 확률을 장기적으로 발생하는 사건의 빈도로 봄
- MLE (최대 우도 추정)를 사용하여 모델의 파라미터 추정. 주어진 데이터에서 발생 가능성이 가장 높은 모수 (Ex. 평균, 분산 등)를 선택하는 방식
- 가설 검정이 자주 사용됨. 시계열 데이터에서 특정 효과의 유의성 검정 또는 모델의 정확성 테스트하는 등의 목적으로 사용 가능
- 여러 번의 실험, 관찰을 통해 알게된 사건의 확률을 검정하므로 사건이 독립적, 반복적, 정규 분포형태일 때 사용하는 것이 좋음
- 대용량 데이터를 쉽게 처리할 수 있음
- 데이터가 부족하거나 불확실 할 경우, 실험 결과도 불확실함.
- Ex. ARIMA
- 베이지안
- 확률은 사건 발생에 대한 믿음 또는 척도
- 불확실성을 확률적으로 표현
- 사전 분포를 이용하여 베이즈 정리를 이용하여 사후 분포를 계산
- 신뢰 구간이 아니라 신뢰 구간의 확률적 버전인 신용 구간을 제공하며, 예측 분포를 통해 미래 값의 불확실성을 평가할 수 있음.
- 과거에는 연산량이 많아서 구현이 어려웠으나, 컴퓨터 연산 능력이 발전됨에 따라 통계/머신러닝 분야에서 많이 사용됨.
- Ex. Prophet, Causal Impact
이처럼 베이지안 방법론은 사전 분포를 이용하여 사후 분포를 계산한다는 점과 불확실성을 확률적으로 표현한다는 점에서 Causal Impact 방법론에 적절한 통계적 접근 방식이라고 할 수 있다. (특정 이벤트 발생 전후의 개입 효과가 목표이기 때문)
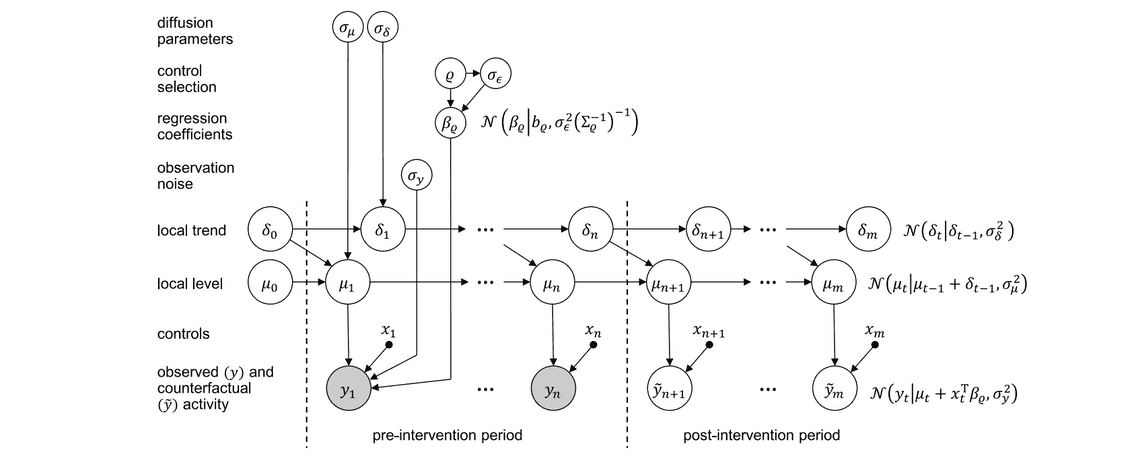
Causal Impact 내에서 사용되는 BSTS 모델의 내부 구조로는 크게 트렌드, 계절성, 회귀 모형이라는 3가지 상태 컴포넌트로 구성되어 있다.
- 트렌드: 장기적인 추세를 모델링
- 계절성: 주기적 패턴 학습 (시즌의 길이를 임의로 조정하여 학습 가능. Ex. 시즌 길이가 7일 경우, 일별 데이터에서 요일 효과를 얻을 수 있음)
- 회귀 모형: 모델링하려는 시계열 데이터에 영향을 미치는 외부 변수들과의 관계 정의. 외부 변수들을 활용하여 회귀 예측의 정확성을 향상시키는 역할
위의 컴포넌트로 모형을 구성하면 데이터를 통해 파라미터를 추론할 수 있으며, 파라미터 추론은 아래의 세 단계로 진행된다.
- MCMC (Markov Chain Monte Carlo) 방식의 통계적 샘플링 알고리즘을 사용하여 특정 이벤트 개입 이전의 관측 데이터를 바탕으로 모형 파라미터와 상태 벡터를 시뮬레이션
- 개입 이전의 목표 시계열과 전체 기간의 공변량을 반영하여 개입이 없었을 경우의 시계열 분포 시뮬레이션
- 2번 단계에서 수행한 posterior 샘플링 결과를 통해 시점 별 인과 효과와 누적 인과 효과의 사후 분포 도출
파라미터 추론 후, 인과 효과를 개선하는 방식은 아래와 같이 활용할 수 있다.
- 이벤트 발생 시점 이후, 실제 시계열 데이터와 개입이 없을 경우 예측된 시계열 데이터 간의 시점 별 차이 (Impact) 도출
- 개입 이후 누적 효과 계산 (Ex. 누적 회원가입 수, 매출 등)
Causal Impact 모형의 가정 검증 방법
- 모형에 적용된 공변량의 개입 영향 파악. 예측값에 영향을 줄만한 변수들의 영향 파악 필요
- 이벤트 발생 또는 개입 시점 이전의 시계열 예측이 올바른지 확인 필요 (이벤트 발생 시점 이전의 예측 정확도)
- 이벤트 발생 또는 개입 시점 이후의 예측값 추이가 실제 값과 어떻게 차이가 나는지 비교 분석 (Ex. 회원 할인 쿠폰 발행 후, 쿠폰 발행 이벤트가 없었더라면 신규 회원 가입이 감소했을 것이라고 가정)
