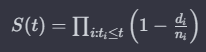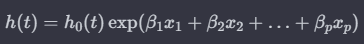목차

• 생존 분석 기법
• 머신러닝 방법론
• 성능 지표

1. 생존 분석 기법

그림 1에서 보이는 것처럼 생존 분석에는 크게 4가지의 기법으로 나뉜다.

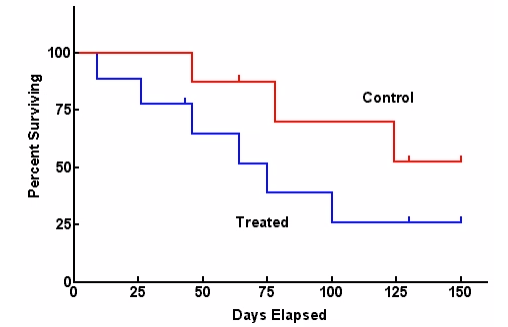
• Non-parametric: 데이터의 독립 변수와 생존 시간 분포를 모두 사용하지 않는 방법. 분포 정보를 알 수 없을 때 유용하지만 예측이 부정확 할 수 있음 (Ex. Kaplan-Meier)
• Semi-parametric: 데이터의 독립 변수는 사용, 생존 시간 분포 정보는 사용하지 않는 방법. (Ex. Cox 비례 위험 모형)
• Parametric: 생존 시간 분포가 존재한다고 가정하고 회귀 모델로 생존 시간을 예측. (Ex. 지수 분포, 로지스틱 분포, Weibull 분포)
• Machine Learning: 머신러닝 알고리즘을 생존 분석에 적용한 기법. 비선형 관계에 있는 독립 변수를 사용하여 모델링이 가능함

그림1에 나와있듯, 다양한 생존분석 방법론들이 존재하나, 여기서는 Machine Learning을 활용한 분석 방법에서 SVM과 앙상블 기법에 대해 자세히 다뤄볼 예정이다.

2. 머신러닝 방법론

2.1) Survival SVM (Support Vector Machine)

SVM은 데이터에 존재하는 클래스 간의 경계를 찾는 지도학습 알고리즘이다. 클래스를 나누는 결정 경계는 클래스 간의 간격 (마진)을 최대화하는 것이 목표라고 할 수 있다. SVM에 대한 자세한 설명은 머신러닝 챕터에서 소개할 예정이고 주요 개념만 써보겠다.

<SVM 주요 개념>

• 결정 경계: 주어진 데이터를 나누는 역할. 클래스 간의 간격 (마진)을 최대화하는 것이 목표 (보통의 그림에는 x, y 축에는 주어진 데이터의 변수들이 들어간다고 이해할 수 있음)
• 서포트 벡터: 결정 경계에 가장 가까이 있는 데이터 포인트. 결정 경계의 모양 결정하는데 주요 역할
• 커널 트릭: 데이터를 고차원으로 매핑하여 비선형 결정 경계 탐색 (Ex. Radial Basis Function Kernel)
• 마진: 결정 경계와 서포트 벡터 사이의 거리. 이 마진을 최대화할수록 좋은 성능가진 SVM이라고 할 수 있음
  • 하드 마진: 데이터가 완벽하게 선형적으로 나누어진 경우, 이상치에 민감
  • 소프트 마진: 일부 오차 허용하여 일반화 성능을 향상

Survival SVM은 크게 두 가지 접근법으로 사용될 수 있다. 주어진 데이터의 독립변수들을 이용하여,

• 순위 문제: 주어진 데이터의 모든 샘플 쌍을 고려하여 생존 시간이 더 짧은 샘플을 더 낮은 순위로 할당 (샘플 aka 데이터 포인트), 해당 샘플이 순위가 낮을수록 이벤트가 발생할 가능성 (발생 위험도)이 높다고 가정
  • 장점: 이벤트가 드물게 발생하는 경우에도 상대적인 순위 기반으로 학습 가능
  • 단점
    • 해석의 어려움: 특정 순위 부여한 이유를 명확히 알기 어려움
    • 제한된 정보: 명확한 생존 확률 또는 시간 정보가 제공되지 않고 각 샘플 간의 상대적인 순위만 나오므로 해석이 모호함.
• 회귀 문제: 주어진 데이터들의 생존 시간을 직접 예측
  • 장점
    • 해석 용이: 각 독립 변수의 회귀 계수를 통해 각 변수의 영향도 추정 가능
    • 기존 회귀 모델과의 비교 용이함
  • 단점
    • 이벤트 적은 경우, 적절한 예측 수행이 어려움 (데이터 이벤트 발생 여부 클래스 불균형 발생)
    • 제약된 선형 가정: 회귀 예측 특성 상, 독립 변수와 종속 변수 간의 선형 관계를 가정. 생존 데이터의 특성 상 부합하지 않을 수도 있음

2.2) Ensemble Learning

그림 2에 나와있듯, 앙상블 기법에는 부스팅, 배깅, 스태킹 총 3가지의 알고리즘이 있다.

• 부스팅: 일련의 모델이 순차적으로 학습되며 각 모델은 이전 모델의 오류를 수정, 잘못 분류된 샘플의 가중치를 증가시켜 다음 모델에서 개선시키는 알고리즘 (Ex. AdaBoost)
• 배깅: 훈련 데이터를 무작위 중복 허용하여 하위 집합을 만든 후 (bootstrap sampling), 독립적으로 동일한 모델을 학습. 이 때, 회귀 모델의 경우 각 모델 예측 값 평균, 분류일 경우 다수결 투표 등을 통해 최종 예측 결정 (Ex. Random Forest)
• 스태킹: 훈련 데이터에 대하여 서로 다른 모델을 훈련시킨 후, 각 모델들의 예측 결과를 새로운 변수로 사용하여 메타 모델을 학습. 메타 모델은 각 모델들의 예측을 바탕으로 최종 예측 수행

2.2.1) Random Survival Forest

Random Survival Forest는 기존 Random Forest 모델에서 생존 분석에 맞게 변형한 모델이다.

간략한 동작 순서는

1. Bootstrap Sampling: Bootstrap 샘플링을 통해 무작위로 선택된 데이터로 구성하여 트리를 생성
2. 무작위 독립 변수 선택: 무작위로 선택된 독립 변수를 사용하여 트리를 분할
3. 이벤트 트리 구성: 이벤트 트리는 각 노드에서 특정 시간 구간에 이벤트가 발생할 확률을 계산
4. 생존 함수 예측: 각 트리의 이벤트 트리를 통해 개별 관측치에 대한 생존 함수 예측. 모든 트리에서의 예측을 종합하여 최종적인 생존 함수 형성 (생존 함수: 주어진 시간에 대해 이벤트가 발생하지 않을 확률)

최종적으로 생성된 생존 함수를 통해 Random Survival Forest에서는 위험도를 추정할 수 있다.

2.3) 성능 지표

2.3.1) Concordance Index (C-index)

단순히 예측시간에 대한 정확도만 보고싶을 경우에는 MSE와 같은 지표를 사용해도 되지만, 이벤트 발생 여부에 대한 것도 같이 고려하기 위해서는 다른 성능지표가 필요하다.

C-index는 이벤트가 발생하기까지 걸리는 시간과 함께 이벤트 발생 여부도 같이 고려한다는 점에서 생존 분석에서 자주 사용되는 성능 지표다.

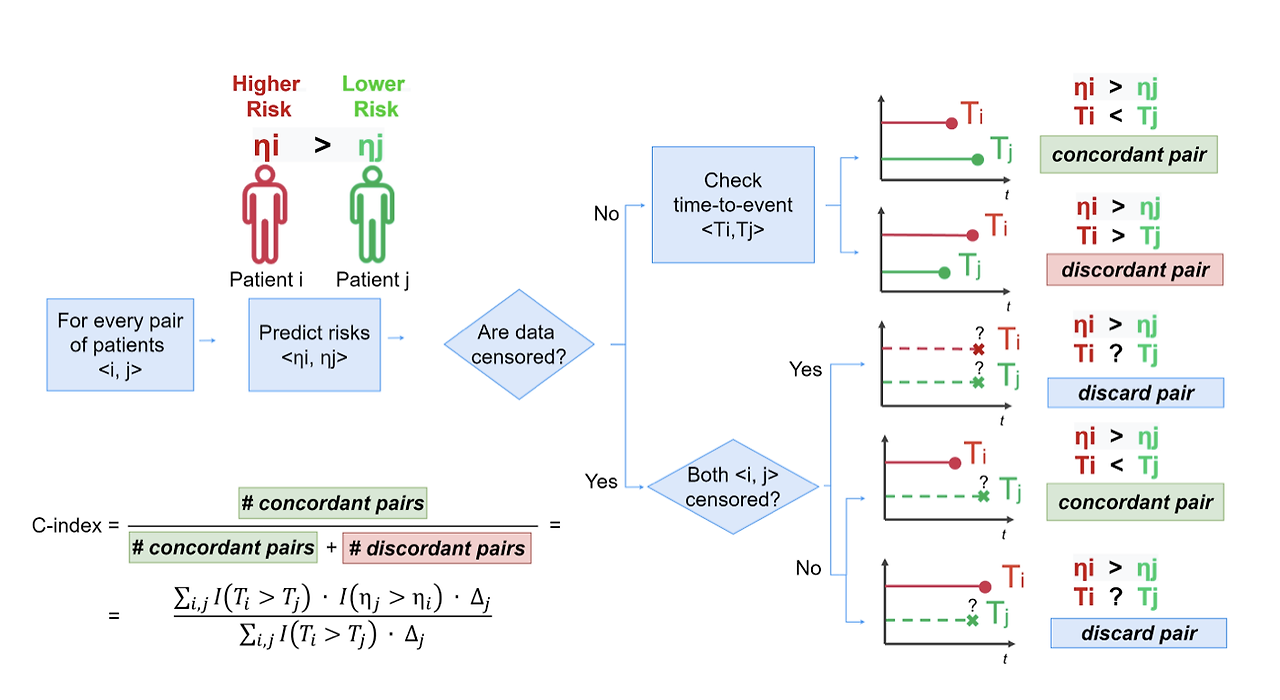
C-index에서는 두 관측치 간의 비교를 통해 모델의 성능을 평가한다. 두 관측치를 쌍 (A, B)으로 구성하는데,

• 관측치 A가 관측치 B보다 위험도가 더 높게 예측된 경우, 관측치 A의 생존 시간이 관측치 B보다 생존시간이 짧을 경우
• 관측치 A가 관측치 B보다 위험도가 더 낮게 예측된 경우, 관측치 A의 생존 시간이 관측치 B보다 생존시간이 길 경우

올바르게 예측했다고 간주하고 성능 지표를 계산한다. (그림 3의 concordant pair)

반대의 경우에는 틀리게 예측했다고 계산한다. (그림 3의 discordant pair)

다만, 두 관측치가 모두 중도절단되거나 한 관측치가 이벤트 발생한 시점보다 더 일찍 중도절단되었을 경우 계산에 포함되지 않는다. (그림 3의 discard pair)

C-index는 0~1 사이의 값을 갖게 되며, 1에 가까울수록 모델의 성능이 좋다고 해석된다. 0.5에 가까울수록 무작위로 예측했다고 해석할 수 있다.

2.3.2) Brier Score

Brier Score는 모델의 생존 예측 확률과 실제 이벤트 발생 여부 간의 평균 제곱 차이를 측정하는 지표다.

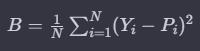
• N: 관측치 수
• Y(i): i번째 관측치의 실제 이벤트 발생 여부를 나타내는 이진 변수 (이벤트 발생 시 1, 아니면 0)
• P(i): i번째 관측치에 대한 모델의 생존 예측 확률

0~1 사이의 값을 가지며, 값이 작을수록 모델의 예측이 더 정확하다고 해석된다.

목차

• 생존 분석 개념
• 생존 분석 방법

1. 생존 분석 개념

•  생존 분석은 특정 대상의 사건 발생 시간을 다루는 통계 분석 방법론
•  어떠한 사건이 발생하기까지 걸리는 시간을 추정
•  기존에는 의학 분야에서 환자들의 생존 가능성 추정에 많이 사용되었지만, 최근에는 제품 수명 예측, 고객 이탈률 등 다양한 분야에서도 많이 활용됨

 <주요 키워드>

• 생존: 특정 사건이 아직 발생하지 않은 상태
• 시간 (Time): 상대적 시간을 의마함. 분석하려는 대상을 관찰하기 시작한 시점으로부터 경과한 시간
• 사건 (Event): 생존의 반대 상태. 사망, 고객 이탈 등 생존 분석을 하기 위한 대상이라고 해석. 생존 분석에서는 오로지 한 번만 발생 (사건 발생 or 발생하지 않음)
• 중도절단 (Censored): 관찰을 시작하기 전, 후로 나누어 해석 가능
  
  • Right Censored: 대상에 아직 사건이 발생하지 않거나, 기타 이유로 관찰이 종료된 것. 실제 생존 시간이 관찰 기간보다 긴 경우를 의미함
  • Left Censored: 대상을 관찰하기 전에 이미 사건이 발생 또는 기대한 최소 기간보다 생존 기간이 더 짧은 경우
• 생존함수 (Survival Function): 관찰 대상이 특정 시점보다 더 오래 생존 (사건이 발생하지 않을)할 확률을 계산하는 함수 (누적 생존 확률)
• 위험함수 (Hazard Function): 특정 시점에 사건이 발생할 확률. 이 때, 사건이 발생하기 전에는 해당 사건이 발생하면 안됨. 대상이 특정 시점까지 생존한 상태에서 특정 시점에 사건이 발생할 확률​
• 누적위험함수 (Cumulative Hazard Function): 위험함수를 관찰을 시작한 시점부터 사건이 발생한 시점까지 적분한 값. 즉, 사건 발생 시점 전까지 관찰 대상에게 사건이 발생할 확률을 각각의 시점마다 구한 후, 모두 더한 것

2. 생존 분석 방법

2.1) Kaplan-Meier 추정

• 추정 방법: 관찰 시간에 따라 사건이 발생한 시점의 사건 발생률 계산, 시간에 따른 생존 함수를 추정
  
  1. 데이터를 시간에 따라 정렬
  2. 각 시점마다 생존해 있는 사람 수와 관찰 대상 그룹에 속한 사람 수 정리 (관찰 대상 그룹에는 관찰이 중단된 사람, 생존해 있는 사람, 사건이 일어난 사람 세 부류가 있다)

• 수식
  • S(t): 시간 t에서의 생존 확률
  • t(i): 이벤트가 발생한 시간의 집합
  • d(i): 시간 t(i)에서 이벤트가 발생한 개수
  • n(i): 시간 t(i)에서 생존 가능한 개체의 수

• 특징
  • 이벤트가 발생하지 않는 시간까지 각 시간의 생존 확률 계산
  • 이벤트가 발생한 시간에서의 생존 확률 S(t)는 해당 시간 직전까지의 누적확률에 현재 시간에서의 생존 확률을 곱한 것
  • 사건이 발생하지 않은 관측치에 대해서도 누적 확률 도출 가능
  • 다양한 시점에서 사건이 발생할 수 있는 경우에 유용함
  • 두 그룹의 생존하는 비율 차이 비교에 사용됨 (실험군 vs 대조군 비교 시, 신뢰구간 비교)
  • 비모수적 추정 방법
    • 비모수적 통계방법: 확률 분포에 대한 가정을 하지 않고, 데이터의 분포나 특성에 대한 일반적인 추론을 수행하는 통계적 방법, 관측값의 순위 또는 분포를 사용하여 추론 수행, 특정한 가정 없이 데이터를 다룰 수 있음
    • 모수적: 특정한 확률 분포를 기반으로 모집단의 특성을 추정

2.2) Log Rank Test

• 추정 방법: 생존 함수 분포를 비교하고 유의한 차이가 있는지 알아보는 가설 검정 기법
  
  • Kaplan-Meier 생존 곡선 [그림 1]을 사용하여 그룹 간의 생존 분포가 통계적으로 유의미한 차이가 있는지 확인
  • 각 그룹에서 발생한 사건의 수와 관측치 수를 이용하여 기대되는 사건의 수와 실제로 발생한 사건의 수 간의 차이를 검정

• 수식
  • 예상 이벤트: 특정 시간에서 그룹 내 발생할 것으로 예상되는 사건의 수, 특정 시간에서의 생존 확률과 그 시간 간격을 곱하여 계산
  • 실제 이벤트: 해당 시간에서 그룹 내에서 실제로 발생한 사건 수

2.3) Cox 비례 위험 모형 (Cox Proportional Hazard Model)

• 추정 방법
  • 생존 시간에 영향을 미치는 요인들의 효과 추정
  • 변수들 간의 비례적 위험 가정: 위험비(변수 한 단위가 변화할 때 변화하는 위험함수 값)가 생존 기간 내내 시간과 무관하게 일정하다고 가정
  • 설명 변수들의 위험 비율이 시간에 따라 변하지 않고 일정하다고 가정 (단, 생존에는 영향을 주는 변수)
  • Hazard: 위험률, 어느 시점에 대상이 탈락가능성이 높은지 평가하는 비율

• 수식
  • h(t): 시간 t에서의 위험 비율 (두 그룹 간의 위험의 상대적 크기)
  • h0(t): 기준 위험 비율
  • x1, x2, ..., xp: 독립 변수
  • beta1, beta2, ..., betap: 설명 변수의 회귀 계수
• 특징
  • Kaplan-Meier, Log-Rank Test와 달리, 설명 변수들의 함수 형태나 생존 곡선의 형태에 대한 가정을 하지 않음, 모델이 더 유연하게 다양한 데이터에 적용 가능
  • 비례적 위험 가정
  • 독립 변수 여러 개 고려 가능
  • Semi Parametric: 독립 변수 정보를 활용하지만, 생존 시간 분포 정보를 사용하지 않는 방법 (Kaplan-Meier 추정은 Non-Parametric, 독립변수와 생존 시간 분포 정보 모두 사용 안함, 분포 정보를 알 수 없을 때 유용하지만 예측이 부정확할 수 있음)